КГД уравнения (QGD equations)
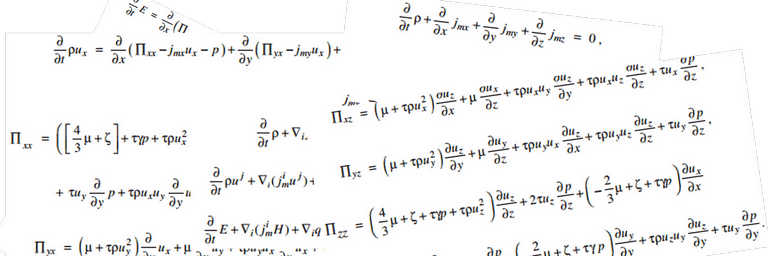
О квазигазодинамических и квазигидродинамических (КГД) уравнениях
Квазигазодинамических уравнений впервые появилась в ходе исследований, выполненных в восьмидесятых годах группой специалистов Института прикладной математики им. М.В.Келдыша под руководством профессора, а ныне члена корреспондента Российской Академии Наук Б.Н.Четверушкина.
В работах этой группы были построены оригинальные разностные схемы для решения уравнений газовой динамики, которые опирались на известную кинетическую модель, трактующую движение частиц газа как совокупность циклически повторяющихся процессов бесстолкновительного разлета частиц с последующей мгновенной релаксацией к локально-равновесному состоянию.
В 1983 г. мне посчастливилось включиться в эту работу, в результате чего на основе указанной кинетической модели был выписан первый вариант КГД уравнений. Эти уравнения отличались от уравнений Эйлера дополнительными слагаемыми, имеющими вид вторых пространственных производных, которые позволяли строить эффективные численные алгоритмы решения задач газовой динамики в рамках уравнений Эйлера, а впоследствии и уравнений Навье-Стокса.
Позднее в работах Ю.В.Шеретова был предложен феноменологический вывод квазигазодинамических и родственных им квазигидродинамических уравнений на аксиоматической основе. Принципиальным и существенным отличием от теории Навье-Стокса является использование процедуры пространствено-временного осреднения для определения основных газодинамических величин – плотности, скорости и температуры [Шеретов Ю.В Математическое моделирование течений жидкости и газа на основе квазигидродинамических и квазигазодинамических уравнений. Тверь: Тверской гос. ун-т, 2000].
Обе КГД системы успешно использовались в задачах численного моделирования течений жидкости и газа. Кроме того, были построены различные обобщения КГД систем. В частности, обобщения квазигазодинамической системы на случаи температурно-неравновесных течений газа и бинарной смеси газов, и квазигидродинамическая модель течений электропроводной жидкости в электромагнитном поле.
Проведенные исследования выполнены в соавторстве с Борисом Николаевичем Четверушкиным, Андреем Николаевичем Павловым, Александром Николаевичем Антоновым, Максимом Александровичем Антоновым, Ириной Александровной Граур, Юрием Владимировичем Шеретовым, Семеном Викторовичем Цынковым, Леонидом Витальевичем Косаревым, Ильей Владимировичем Абалакиным, Людвигом Вацлавовичем Дородницыным, Дмитрием Борисовичем Гуровым, Аскаром Есимкуловичем Дуйсекуловым, Анной Викторовной Ключниковой, Иваном Анатольевичем Широковым, Татьяной Алексеевной Кудряшовой, Марией Евгеньевной Соколовой, Ириной Станиславовной Калачинской, Евгением Владимировичем Шильниковым, Ольгой Юрьевной Милюковой, Жан-Клодом Ленграном, Амером Шпуном, Сальвадором Монтеро и Региной Вебер, которым я глубоко благодарна за сотрудничество.
About quasi-gasdynamic (QGD) and quasi-hydrodynamic (QHD) equations

The quasi-gasdynamic system of equations was obtained by the Institute for the Applied mathematics (Russian Academy of Science) research group, leaded by Prof. Chetverushkin, subsequently RAS corresponding member.
First, original finite-difference schemes for gasdynamic equations were constructed. These schemes used a well-known kinetic model treating the behavior of gas particles as a cyclic process of collisionless motion followed by instant relaxation to local equilibrium.
In 1983, I joined this work and the first variant of quasi-gasdynamic equations based on the forgoing kinetic model was obtained. These equations, unlike the Eiler equations, contained items with second spatial derivatives. The numerical algorithms based on this approach proved to be very efficient in computations of complex gasdynamic problems.
A phenomenological postulational derivation of quasi-gasdynamic and quasi-hydrodynamic equations was given by Sheretov [Sheretov Yu.V. Matematicheskoe modelirovanie techenii zhidkosti i gaza na osnove kvazigidrodinamicheskikh i kvazigazodinamicheskikh uravnenii (Quasi-hydrodynamic and quasi-gasdynamic equations based mathematical modeling of liquid and gas flows). Tver: Tver State University. 2000]. Unlike the Navier-Stokes theory, this approach uses spatial-temporal averaging for the main gasdynamic parameters: density, velocity and temperature.
Both QGD and QHD systems were used successfully in gasdynamic and hydrodynamic numerical simulation. Also, some generalizations of both systems were constructed. For example, QGD system was extended to gases with thermal nonequilibrium and to binary gas mixtures, and QHD system was generalized to electroconductive liquid affected by the electromagnetic field.
I would like to thank Boris Nikolaevich Chetverushkin, Andrei Nikolaevich Pavlov, Aleksandr Nikolaevich Antonov, Maksim Aleksandrovich Antonov, Irina Alexandrovna Graur, Yurii Vladimirovich Sheretov, Semion Viktorovich Tsynkov, Leonid Vitalievich Kosarev, Ilia Vladimirovich Abalakin, Liudvig Vatslavovich Dorodnitsyn, Dmitrii Borisovich Gurov, Askar Esimkulovich Duisekulov, Anna Viktorovna Kliuchnikova, Ivan Anatolievich Shirokov, Tatiana Alekseevna Kudriashova, Maria Evgenievna Sokolova, Irina Stanislavovna Kalachinskaia, Evgenii Vladimirovich Shilnikov, Olga Yurievna Miliukova, Jean-Claude Lengrand, Amer Chpoun, Salvador Montero and Regine Weber for cooperation.